Attention

attention有很多种形态，大家通常会说5种：hard attention，soft attention，Global Attention，local attention，self attention。

hard attention ： Hard Attention不会选择整个encoder的隐层输出做为其输入，它在t时刻会依多元伯努利分布来采样输入端的一部分隐状态来进行计算，而不是整个encoder的隐状态。在 hard attention 里面，每个时刻 t 模型的序列 [ St1,…,StL ] 只有一个取 1，其余全部为 0，是 one-hot 形式。也就是说每次只focus 一个位置。

soft attention ： 对于hard attention，soft attention 每次会照顾到全部的位置，只是不同位置的权重不同罢了。

global attention ： global attention 顾名思义，forcus 全部的 position。它 和 local attention 的主要区别在于 attention 所 forcus 的 source positions 数目的不同。

Local Attention : Local Attention只 focus 一部分 position，则为 local attention global attention 的缺点在于每次都要扫描全部的 source hidden state，计算开销较大，为了提升效率，提出 local attention，每次只 focus 一小部分的 source position。

self attention

动机：说起self-attention的提出，是因为rnn存在非法并行计算的问题，而cnn存在无法捕获长距离特征的问题，因为既要又要的需求，当看到attention的巨大优势，《Attention is all you need》的作者决定用attention机制代替rnn搭建整个模型，于是Multi-headed attention，横空出世。

Self-Attention原始的形态：$softmax(XX^T)X$

  • $XX^T$是一个矩阵乘以它自己的转置，可以看成矩阵的每个向量分别与其他向量计算内积。

  • 向量的内积表征两个向量的夹角，表征一个向量在另一个向量上的投影。投影的值大，说明两个向量相关度高。

  • 更进一步，这个向量是词向量，是词在高维空间的数值映射。词向量之间相关度高表示什么？是不是在一定程度上（不是完全）表示，在关注词A的时候，应当给予词B更多的关注？

  • 矩阵$XX^T$ 是一个方阵，我们以行向量的角度理解，里面保存了每个向量与自己和其他向量进行内积运算的结果。

  • softmax的作用是归一化。Attention机制的核心就是加权求和，权重就是归一化得到的。

  • 最后乘以$X$，得到的结果中的每一个行向量都是词向量经过注意力机制加权求和之后的表示。

image-20210829115751302

注意力头的维度是默认64.

img

Attention的计算方法：

image-20210829121024997

Q K V矩阵

  • 其来源是X与矩阵的乘积，本质上都是X的线性变换。不直接使用X而对其进行线性变换是为了提升模型的拟合能力，矩阵W都是可以训练的，起到一个缓冲的效果。

  • Query，Key，Value的概念取自于信息检索系统，举个简单的搜索的例子来说。当你在某电商平台搜索某件商品（年轻女士冬季穿的红色薄款羽绒服）时，你在搜索引擎上输入的内容便是Query，然后搜索引擎根据Query为你匹配Key（例如商品的种类，颜色，描述等），然后根据Query和Key的相似度得到匹配的内容（Value)。

  • Q表示为了编码当前词，需要去注意(attend to)其它(其实也包括它自己)的词，我们需要有一个查询向量。而Key向量可以认为是这个词的关键的用于被检索的信息，而Value向量是真正的内容。

  • self-attention中的Q，K，V也是起着类似的作用，在矩阵计算中，点积是计算两个矩阵相似度的方法之一，因此式1中使用了$QK^T$进行相似度的计算。接着便是根据相似度进行输出的匹配，这里使用了加权匹配的方式，而权值就是query与key的相似度。

关于为什么要除以注意力头的维度？

  • 假设 Q 和 K 的均值为0，方差为1。它们的矩阵乘积$A^T=Q^TK$将有均值为0，方差为dk。当dk变得很大时，A中的元素的方差也会变得很大，如果A中的元素方差很大，那么softmax(A)的分布会趋于陡峭(分布的方差大，分布集中在绝对值大的区域)。总结一下就是softmax(A)的分布会和d有关。因此A中每一个元素除以dk的平方根后，方差又变为1.这使得softmax(A)的分布“陡峭”程度与d解耦，从而使得训练过程中梯度值保持稳定。

  • 参考：transformer中的attention为什么scaled?

为什么用点乘而不是加性的attention？

  • 常用的attention有加性的和点乘性的。这里用的是点乘（多了个scaling factor ）。理论上这两者的复杂度是相似的，但实际上点乘速度更快，空间效率也更高，因为它可以用高度优化的矩阵乘积来实现。

  • 对于小的dk，两种机制表现相似，但是对于值更大的dk（不做scaling），加性的表现更好。（来自Transformer论文）

Multi-attention

  • 对于输入矩阵(time_step, num_input)，每一组Q、K和V都可以得到一个输出矩阵Z(time_step, num_features)。

  • 但是后面的全连接网络需要的输入是一个矩阵而不是多个矩阵，因此我们可以把多个head输出的Z按照第二个维度拼接起来，但是这样的特征有一些多，因此Transformer又用了一个线性变换(矩阵WO)对它进行了压缩。

image-20210829121454167
img

  • Multi-Head Attention 通过多层的 Self-Attention 可以将输入语句映射到不同的子空间中，于是能够更好地理解到语句所包含的信息。

目的与特点

  • Self-attention的目的是学习句子内部的词依赖关系，捕获句子的内部结构。

  • 而Multi-head Attention其实就是多个Self-Attention结构的结合，每个head学习到在不同表示空间中的特征。

  • 优点：self-attention的特点在于无视词之间的距离直接计算依赖关系，能够学习一个句子的内部结构，实现也较为简单，可以并行计算。

  • 缺点：对self-attention来说，它跟每一个input vector都做attention，所以没有考虑到input sequence的顺序。

  • 原论文中说到进行Multi-head Attention的原因是将模型分为多个头，形成多个子空间，可以让模型去关注不同方面的信息，最后再将各个方面的信息综合起来。其实直观上也可以想到，如果自己设计这样的一个模型，必然也不会只做一次attention，多次attention综合的结果至少能够起到增强模型的作用，也可以类比CNN中同时使用多个卷积核的作用，直观上讲，多头的注意力有助于网络捕捉到更丰富的特征/信息。

最后的问题是，为什么要像公式那样计算呢？

我们先从 QKT 看起，从几何角度看，点积是两个向量的长度与它们夹角余弦的积。如果两向量夹角为90°，那么结果为0，代表两个向量线性无关。如果两个向量夹角越小，两向量在方向上相关性也越强，结果也越大。点积反映了两个向量在方向上的相似度，结果越大越相似。

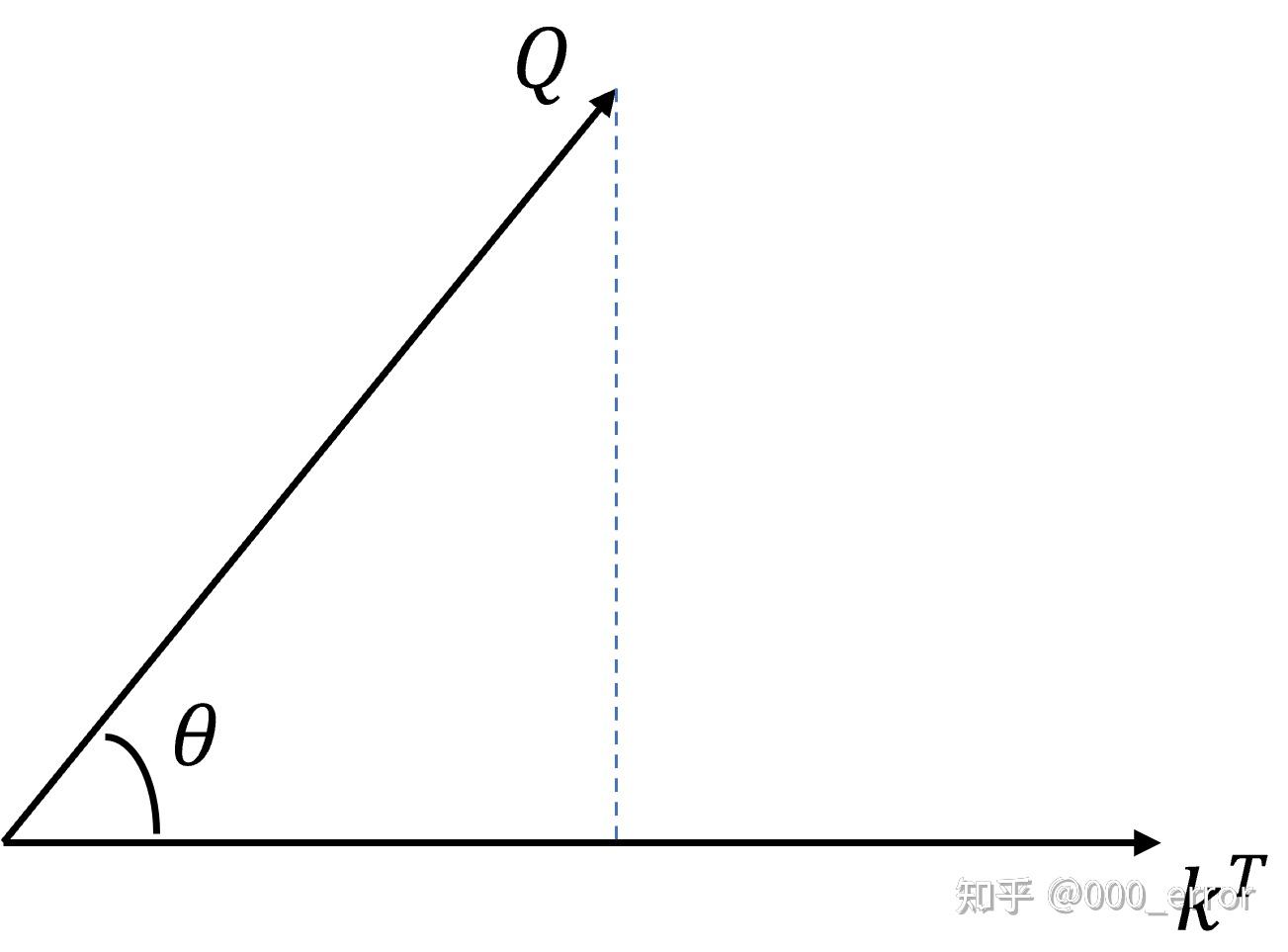
对 QKT 进行相似度的计算后，再使用softmax归一化。最后将归一化的结果与 V 作乘法，计算的结果就是输入经过注意力机制加权求和之后的表示。

代码实现

```python
import torch
import torch.nn.functional as F
 
class SelfAttention(torch.nn.Module):
    def __init__(self, input_dim, heads):
        super(SelfAttention, self).__init__()
        self.input_dim = input_dim
        self.heads = heads
        self.head_dim = input_dim // heads
 
        self.W_q = torch.nn.Linear(input_dim, input_dim)
        self.W_k = torch.nn.Linear(input_dim, input_dim)
        self.W_v = torch.nn.Linear(input_dim, input_dim)
 
        self.W_o = torch.nn.Linear(input_dim, input_dim)
 
    def forward(self, x):
        batch_size = x.shape[0]
 
        # Linear transformation to get Q, K, V
        Q = self.W_q(x)
        K = self.W_k(x)
        V = self.W_v(x)
 
        # Reshape Q, K, V to have multiple heads
        Q = Q.view(batch_size, -1, self.heads, self.head_dim).permute(0, 2, 1, 3)
        K = K.view(batch_size, -1, self.heads, self.head_dim).permute(0, 2, 1, 3)
        V = V.view(batch_size, -1, self.heads, self.head_dim).permute(0, 2, 1, 3)
 
        # Compute attention scores
        scores = torch.matmul(Q, K.permute(0, 1, 3, 2)) / (self.head_dim ** 0.5)
        attention_weights = F.softmax(scores, dim=-1)
 
        # Apply attention weights to V
        attention_output = torch.matmul(attention_weights, V)
 
        # Reshape and concatenate heads
        attention_output = attention_output.permute(0, 2, 1, 3).contiguous()
        attention_output = attention_output.view(batch_size, -1, self.input_dim)
 
        # Final linear transformation
        output = self.W_o(attention_output)
 
        return output
 
# 使用示例
input_dim = 64
seq_length = 10
heads = 8
input_data = torch.randn(1, seq_length, input_dim)  # 生成随机输入数据
self_attention = SelfAttention(input_dim, heads)
output = self_attention(input_data)
print(output.shape)  # 输出形状：torch.Size([1, 10, 64])

参考资料

白话attention（上）

超详细图解Self-Attention的那些事儿

[浅谈] 分析一下各种softmax attention的变种

手写 Self-Attention 的四重境界，从 self-attention 到 multi-head self-attention | chaofa用代码打点酱油

PreviousBaseNextMask

Last updated

Was this helpful?