位置编码

有两个选择：1、想办法将位置信息融入到输入中，这构成了绝对位置编码的一般做法；2、想办法微调一下Attention结构，使得它有能力分辨不同位置的Token，这构成了相对位置编码的一般做法。

绝对位置编码

一般来说，绝对位置编码会加到输入中：在输入的第k个向量xk中加入位置向量pk变为xk+pk，其中pk只依赖于位置编号k。

训练式

• 直接将位置编码当作可训练参数

• 比如最大长度为512，编码维度为768，那么就初始化一个512×768的矩阵作为位置向量，让它随着训练过程更新。

• 例子：BERT、GPT，2017年Facebook的《Convolutional Sequence to Sequence Learning》

• 缺点是没有外推性，即如果预训练最大长度为512的话，那么最多就只能处理长度为512的句子，再长就处理不了了。

• 也可以将超过512的位置向量随机初始化，然后继续微调。

• 通过层次分解的方式，可以使得绝对位置编码能外推到足够长的范围，同时保持还不错的效果

• 《层次分解位置编码，让BERT可以处理超长文本》

三角式

三角函数式位置编码，一般也称为Sinusoidal位置编码，是Google的论文《Attention is All You Need》所提出来的一个显式解：

image-20210828225320408

• 相邻的位置编码向量很相似，较远的位置编码向量差异很大，说明基于正余弦函数的绝对位置可以表征位置的相关性；

• 不需要显式地学习位置，提高效率。

Sinusoidal位置编码的每个分量都是正弦或余弦函数，所有每个分量的数值都具有周期性。如下图所示，每个分量都具有周期性，并且越靠后的分量，波长越长，频率越低。这是一个非常重要的性质，基于RoPE的大模型的长度外推工作，与该性质有着千丝万缕的关联

Sinusoidal位置编码还具有远程衰减的性质，具体表现为：对于两个相同的词向量，如果它们之间的距离越近，则他们的内积分数越高，反之则越低。如下图所示，我们随机初始化两个向量q和k，将q固定在位置0上，k的位置从0开始逐步变大，依次计算q和k之间的内积。我们发现随着q和k的相对距离的增加，它们之间的内积分数震荡衰减。

因为Sinusoidal位置编码中的正弦余弦函数具备周期性，并且具备远程衰减的特性，所以理论上也具备一定长度外推的能力。

固定d为100，维度i=10，绘制不同base下的position embedding，如下图所示：

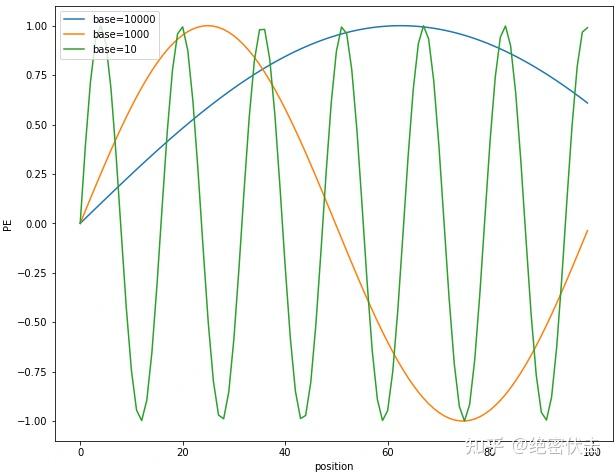
图2-2 不同base下的position embedding取值

可以看到随着base的变大，周期会明显变长。Transformer选择比较大的base=10000，可能是为了能更好的区分开每个位置。

备注：解释下为什么周期大能更好区分位置

从图2-2可以看出，base越大，周期越大。而周期越大，在position从0~100范围内，只覆盖了不到半个周期，这使得重复值少；而周期小的，覆盖了多个周期，就导致不同位置有大量重复的值。

递归式

原则上来说，RNN模型不需要位置编码，它在结构上就自带了学习到位置信息的可能性（因为递归就意味着我们可以训练一个“数数”模型），因此，如果在输入后面先接一层RNN，然后再接Transformer，那么理论上就不需要加位置编码了。同理，我们也可以用RNN模型来学习一种绝对位置编码，比如从一个向量p0出发，通过递归格式p(k+1)=f(pk)来得到各个位置的编码向量。

ICML 2020的论文《Learning to Encode Position for Transformer with Continuous Dynamical Model》把这个思想推到了极致，它提出了用微分方程（ODE）dpt/dt=h(pt,t)的方式来建模位置编码，该方案称之为FLOATER。显然，FLOATER也属于递归模型，函数h(pt,t)可以通过神经网络来建模，因此这种微分方程也称为神经微分方程。

理论上来说，基于递归模型的位置编码也具有比较好的外推性，同时它也比三角函数式的位置编码有更好的灵活性（比如容易证明三角函数式的位置编码就是FLOATER的某个特解）。但是很明显，递归形式的位置编码牺牲了一定的并行性，可能会带速度瓶颈。

相乘式

xk⊗pk的方式

参考《中文语言模型研究：(1) 乘性位置编码》

相对位置编码

相对位置并没有完整建模每个输入的位置信息，而是在算Attention的时候考虑当前位置与被Attention的位置的相对距离，由于自然语言一般更依赖于相对位置，所以相对位置编码通常也有着优秀的表现。对于相对位置编码来说，它的灵活性更大，更加体现出了研究人员的“天马行空”。

经典式

相对位置编码起源于Google的论文《Self-Attention with Relative Position Representations》，华为开源的NEZHA模型也用到了这种位置编码，后面各种相对位置编码变体基本也是依葫芦画瓢的简单修改。

一般认为，相对位置编码是由绝对位置编码启发而来，考虑一般的带绝对位置编码的Attention：

image-20210828225833655

这样一来，只需要有限个位置编码，就可以表达出任意长度的相对位置（因为进行了截断），不管pK,pV是选择可训练式的还是三角函数式的，都可以达到处理任意长度文本的需求。

XLNET式

XLNET式位置编码其实源自Transformer-XL的论文《Transformer-XL: Attentive Language Models Beyond a Fixed-Length Context》，只不过因为使用了Transformer-XL架构的XLNET模型并在一定程度上超过了BERT后，Transformer-XL才算广为人知，因此这种位置编码通常也被冠以XLNET之名。

image-20210828230318201

T5式

T5模型出自文章《Exploring the Limits of Transfer Learning with a Unified Text-to-Text Transformer》，里边用到了一种更简单的相对位置编码。思路依然源自展开式(7)(7)，如果非要分析每一项的含义，那么可以分别理解为“输入-输入”、“输入-位置”、“位置-输入”、“位置-位置”四项注意力的组合。如果我们认为输入信息与位置信息应该是独立（解耦）的，那么它们就不应该有过多的交互，所以“输入-位置”、“位置-输入”两项Attention可以删掉

image-20210828230531918

这个设计的思路其实也很直观，就是比较邻近的位置（0～7），我们需要比较得精细一些，所以给它们都分配一个独立的位置编码，至于稍远的位置（比如8～11），我们不用区分得太清楚，所以它们可以共用一个位置编码，距离越远，共用的范围就可以越大，直到达到指定范围再clip。

代码： https://huggingface.co/transformers/v4.10.1/_modules/transformers/models/t5/modeling_t5.html

解析： https://juejin.cn/post/7107516511824117790

_relative_position_bucket函数的功能就是输入一个相对位置i-j，返回其对应的分区类型

• num_buckets种相对位置，将任意多的相对位置信息映射到这些最终类型上

• bidirectional代表双向的含义是左右位置都处于相同的状态(举个例子，左边0～7的位置和右边0～7的位置的编码相同)

• relative_position=pi-pj

• max_exact = num_buckets // 2

• relative_buckets = (relative_position > 0).to(torch.int32) * num_buckets

• is_small = relative_position < max_exact

• relative_postion_if_large=max_exact + (torch.log(relative_position.float() / max_exact)/ math.log(max_distance / max_exact) * (num_buckets - max_exact)

• relative_postion_if_large每个元素最大取num_buckets - 1

• 最终值=relative_buckets+(is_small的时候取relative_position，否则取relative_postion_if_large)

DeBERTa式

DeBERTa也是微软搞的，论文为《DeBERTa: Decoding-enhanced BERT with Disentangled Attention》，一是它正式中了ICLR 2021，二则是它登上SuperGLUE的榜首，成绩稍微超过了T5。

其实DeBERTa的主要改进也是在位置编码上，同样还是从展开式(7)(7)出发，T5是干脆去掉了第2、3项，只保留第4项并替换为相对位置编码，而DeBERTa则刚刚相反，它扔掉了第4项，保留第2、3项并且替换为相对位置编码（果然，科研就是枚举所有的排列组合看哪个最优）：

image-20210828230654016

不过，DeBERTa比较有意思的地方，是提供了使用相对位置和绝对位置编码的一个新视角，它指出NLP的大多数任务可能都只需要相对位置信息，但确实有些场景下绝对位置信息更有帮助，于是它将整个模型分为两部分来理解。以Base版的MLM预训练模型为例，它一共有13层，前11层只是用相对位置编码，这部分称为Encoder，后面2层加入绝对位置信息，这部分它称之为Decoder，还弄了个简称EMD（Enhanced Mask Decoder）；至于下游任务的微调截断，则是使用前11层的Encoder加上1层的Decoder来进行。

其他位置编码

CNN式

尽管经典的将CNN用于NLP的工作《Convolutional Sequence to Sequence Learning》往里边加入了位置编码，但我们知道一般的CNN模型尤其是图像中的CNN模型，都是没有另外加位置编码的，那CNN模型究竟是怎么捕捉位置信息的呢？

答案可能是卷积核的各项异性导致了它能分辨出不同方向的相对位置。不过ICLR 2020的论文《How Much Position Information Do Convolutional Neural Networks Encode?》给出了一个可能让人比较意外的答案：CNN模型的位置信息，是Zero Padding泄漏的！

我们知道，为了使得卷积编码过程中的feature保持一定的大小，我们通常会对输入padding一定的0，而这篇论文显示该操作导致模型有能力识别位置信息。也就是说，卷积核的各向异性固然重要，但是最根本的是zero padding的存在，那么可以想象，实际上提取的是当前位置与padding的边界的相对距离。

不过，这个能力依赖于CNN的局部性，像Attention这种全局的无先验结构并不适用。

复数式

来自ICLR 2020的论文《Encoding word order in complex embeddings》。论文的主要思想是结合复数的性质以及一些基本原理，推导出了它的位置编码形式（Complex Order）为：

image-20210828231028885

代表词jj的三组词向量。你没看错，它确实假设每个词有三组跟位置无关的词向量了（当然可以按照某种形式进行参数共享，使得它退化为两组甚至一组），然后跟位置kk相关的词向量就按照上述公式运算。

你以为引入多组词向量就是它最特立独行的地方了？并不是！我们看到式(11)还是复数形式，你猜它接下来怎么着？将它实数化？非也，它是将它直接用于复数模型！也就是说，它走的是一条复数模型路线，不仅仅输入的Embedding层是复数的，里边的每一层Transformer都是复数的，它还实现和对比了复数版的Fasttext、LSTM、CNN等模型！这篇文章的一作是Benyou Wang，可以搜到他的相关工作基本上都是围绕着复数模型展开的，可谓复数模型的铁杆粉了～

融合式

利用复数的形式，苏神构思了一种比较巧的位置编码，可以将绝对位置编码与相对位置编码融于一体。

image-20210828231346495

image-20210828231503927

RoPE

RoPE（Rotary Position Embedding）的出发点就是“ 通过绝对位置编码的方式实现相对位置编码 ”，或者可以说是实现 相对位置编码和绝对位置编码的结合 。RoPE位置编码通过将一个向量旋转某个角度，为其赋予位置信息。

假设$q_m$ 和$k_n$ 是对应位置的二维行向量（即每个位置都有两个向量来表征位置），因此这个二维向量可以用复数来代替（包括实部和虚部），因此他们的内积可以作为其对应的Attention值。

后面两项的乘积本质就是向量 q（或k）的两个二维行向量，所以上述公式就是q乘以一个旋转矩阵。

内积满足线性叠加性，因此任意偶数维的RoPE，我们都可以表示为二维情形的拼接：

实现

由于RΘ,md的稀疏性，所以直接用矩阵乘法来实现会很浪费算力，推荐通过下述方式来实现 RoPE：

其中⊗是逐位对应相乘，即计算框架中的∗运算。从这个实现也可以看到，RoPE 可以视为是乘性位置编码的变体。

• 当输入一个句子“Enhanced Transformer with Rotary Position Embedding”时，首先获得其Query和Key向量q、 k，其对应的维度均为d，然后对于向量中相邻两个元素为一组，可以得到 d/2组（图中左下部分相同颜色的两个元素作为一组，对于每一组，一个文本则可以得到两个行向量）；

• 获得每个词的绝对位置编号（该句子由6个词，位置编号分别为1，2，3，4，5，6），假设取“Enhanced”单词为例，其第一组元素为θ1，位置为 m=1，那么通过旋转位置编码可以得到新的元素值x1', x2'。

• 所有单词的d/2个组合都按照这种形式进行“旋转”，即可得到新的位置编码（右下角）

代码实现

# 生成旋转矩阵
def precompute_freqs_cis(dim: int, seq_len: int, theta: float = 10000.0):
    # 计算词向量元素两两分组之后，每组元素对应的旋转角度\theta_i
    freqs = 1.0 / (theta ** (torch.arange(0, dim, 2)[: (dim // 2)].float() / dim))
    # 生成 token 序列索引 t = [0, 1,..., seq_len-1]
    t = torch.arange(seq_len, device=freqs.device)
    # freqs.shape = [seq_len, dim // 2] 
    freqs = torch.outer(t, freqs).float()  # 计算m * \theta

    # 计算结果是个复数向量
    # 假设 freqs = [x, y]
    # 则 freqs_cis = [cos(x) + sin(x)i, cos(y) + sin(y)i]
    freqs_cis = torch.polar(torch.ones_like(freqs), freqs) 
    return freqs_cis

# 旋转位置编码计算
def apply_rotary_emb(
    xq: torch.Tensor,
    xk: torch.Tensor,
    freqs_cis: torch.Tensor,
) -> Tuple[torch.Tensor, torch.Tensor]:
    # xq.shape = [batch_size, seq_len, dim]
    # xq_.shape = [batch_size, seq_len, dim // 2, 2]
    xq_ = xq.float().reshape(*xq.shape[:-1], -1, 2)
    xk_ = xk.float().reshape(*xk.shape[:-1], -1, 2)
    
    # 转为复数域
    xq_ = torch.view_as_complex(xq_)
    xk_ = torch.view_as_complex(xk_)
    
    # 应用旋转操作，然后将结果转回实数域
    # xq_out.shape = [batch_size, seq_len, dim]
    xq_out = torch.view_as_real(xq_ * freqs_cis).flatten(2)
    xk_out = torch.view_as_real(xk_ * freqs_cis).flatten(2)
    return xq_out.type_as(xq), xk_out.type_as(xk)

class Attention(nn.Module):
    def __init__(self, args: ModelArgs):
        super().__init__()

        self.wq = Linear(...)
        self.wk = Linear(...)
        self.wv = Linear(...)
        
        self.freqs_cis = precompute_freqs_cis(dim, max_seq_len * 2)

    def forward(self, x: torch.Tensor):
        bsz, seqlen, _ = x.shape
        xq, xk, xv = self.wq(x), self.wk(x), self.wv(x)

        xq = xq.view(batch_size, seq_len, dim)
        xk = xk.view(batch_size, seq_len, dim)
        xv = xv.view(batch_size, seq_len, dim)

        # attention 操作之前，应用旋转位置编码
        xq, xk = apply_rotary_emb(xq, xk, freqs_cis=freqs_cis)
        
        # scores.shape = (bs, seqlen, seqlen)
        scores = torch.matmul(xq, xk.transpose(1, 2)) / math.sqrt(dim)
        scores = F.softmax(scores.float(), dim=-1)
        output = torch.matmul(scores, xv)  # (batch_size, seq_len, dim)
  # ......

实验

我们看一下 RoPE 在预训练阶段的实验效果：

Stage	Max seq length	Batch size	Training steps	Loss	Accuracy
1	512	256	200k	1.73	65.0%
2	1536	256	12.5k	1.61	66.8%
3	256	256	120k	1.75	64.6%
4	128	512	80k	1.83	63.4%
5	1536	256	10k	1.58	67.4%
6	512	512	30k	1.66	66.2%

从上面可以看出，增大序列长度，预训练的准确率反而有所提升，这体现了 RoPE 具有良好的外推能力。

下面是在下游任务上的实验结果：

Model	Validation	Test
BERT-512	64.13%	67.77%
WoBERT-512	64.07%	68.10%
RoFormer-512	64.13%	68.29%
RoFormer-1024	66.07%	69.79%

其中 RoFormer 是一个绝对位置编码替换为 RoPE 的**WoBERT**模型，后面的参数（512）是微调时截断的maxlen，可以看到 RoPE 确实能较好地处理长文本语义。

远程衰减

d = 128;
\[Theta][t_] = 10000^(-2*t/d);
f[m_] = Sum[
    Norm[Sum[Exp[I*m*\[Theta][i]], {i, 0, j}]], {j, 0, d/2 - 1}]/(d/2);
Plot[f[m], {m, 0, 256}, AxesLabel -> {相对距离, 相对大小}]

从图中我们可以可以看到随着相对距离的变大，内积结果有衰减趋势的出现。因此，选择$\theta_i=10000^{\frac{-2i}{d}}$（i为维度索引，d为向量维度），确实能带来一定的远程衰减性。当然，能带来远程衰减性的不止这个选择，几乎任意的光滑单调函数都可以。如果以$\theta_i=10000^{\frac{-2i}{d}}$为初始化，将θ视为可训练参数，然后训练一段时间后发现θ并没有显著更新，因此干脆就直接固定$\theta_i=10000^{\frac{-2i}{d}}$了。

如上图我们可以总结得到一些规律，base的不同取值会影响注意力远程衰减的程度。当base大于500时，随着base的提升，远程衰减的程度会逐渐削弱。但太小的base也会破坏注意力远程衰减的性质，例如base=10或100时，注意力分数不再随着相对位置的增大呈现出震荡下降的趋势。更极端的情况下，当base=1时，其实也就是上面我们提到的，将所有 都设为1的情况，将完全失去远程衰减特性，如下图所示。

图片

‍‍‍‍‍‍‍‍‍‍‍‍

对于base的性质的研究，与大模型的长度外推息息相关，如NTK-Aware Scaled RoPE、NTK-by-parts、Dynamic NTK等长度外推方法，本质上都是通过改变base，从而影响每个位置对应的旋转角度，进而影响模型的位置编码信息，最终达到长度外推的目的。目前大多长度外推工作都是通过放大base以提升模型的输入长度，例如Code LLaMA将base设为1000000，LLaMA2 Long设为500000，但更大的base也将会使得注意力远程衰减的性质变弱，改变模型的注意力分布，导致模型的输出质量下降。如下图所示。

图片

外推性

线性场景

RoPE是目前唯一一种可以用于线性Attention的相对位置编码。这是因为其他的相对位置编码，都是直接基于Attention矩阵进行操作的，但是线性Attention并没有事先算出Attention矩阵，因此也就不存在操作Attention矩阵的做法，所以其他的方案无法应用到线性Attention中。而对于RoPE来说，它是用绝对位置编码的方式来实现相对位置编码，不需要操作Attention矩阵，因此有了应用到线性Attention的可能性。

优势

1. 用一个旋转矩阵rotation matrix来对绝对位置进行编码；与此同时，在自注意力机制中导入显式的位置依赖。

2. 自由的序列长度；

3. 随着相对位置的增大，而逐步延缓退化（=衰减）的inter-token dependency；

4. 用相对位置编码来“武装”线性自注意力。

5. 和相对位置编码相比，RoPE 具有更好的外推性

具体来说，RoPE 使用 旋转矩阵对绝对位置进行编码 ，同时将 显式的相对位置依赖性纳入自注意公式中 。

【核心的两个点，一个是“旋转矩阵”，一个是“显式的相对位置依赖”】。

旋转编码 RoPE 可以有效地保持位置信息的相对关系，即相邻位置的编码之间有一定的相似性，而远离位置的编码之间有一定的差异性。这样可以增强模型对位置信息的感知和利用。这一点是其他绝对位置编码方式（如正弦位置编码、学习的位置编码等）所不具备的，因为它们只能表示绝对位置，而不能表示相对位置。

旋转编码 RoPE 可以通过旋转矩阵来实现位置编码的外推，即可以通过旋转矩阵来生成超过预训练长度的位置编码。这样可以提高模型的泛化能力和鲁棒性。这一点是其他固定位置编码方式（如正弦位置编码、固定相对位置编码等）所不具备的，因为它们只能表示预训练长度内的位置，而不能表示超过预训练长度的位置。

旋转编码 RoPE 可以与线性注意力机制兼容，即不需要额外的计算或参数来实现相对位置编码。这样可以降低模型的计算复杂度和内存消耗。这一点是其他混合位置编码方式（如Transformer-XL、XLNet等）所不具备的，因为它们需要额外的计算或参数来实现相对位置编码。

备注：什么是大模型外推性？

外推性是指大模型在训练时和预测时的输入长度不一致，导致模型的泛化能力下降的问题。例如，如果一个模型在训练时只使用了512个 token 的文本，那么在预测时如果输入超过512个 token，模型可能无法正确处理。这就限制了大模型在处理长文本或多轮对话等任务时的效果。

NTK原始方法，也就是直接拉大rope_base的方法为什么可以提升模型外推能力？

提高base以后可以将远程不衰减的部分，变回衰减。

比如在llama-3.1-8k rope_base = 500000 的第一层下随机抽取两个token的Q，K。我们观察 attention score 和 positional distance的变化曲线：

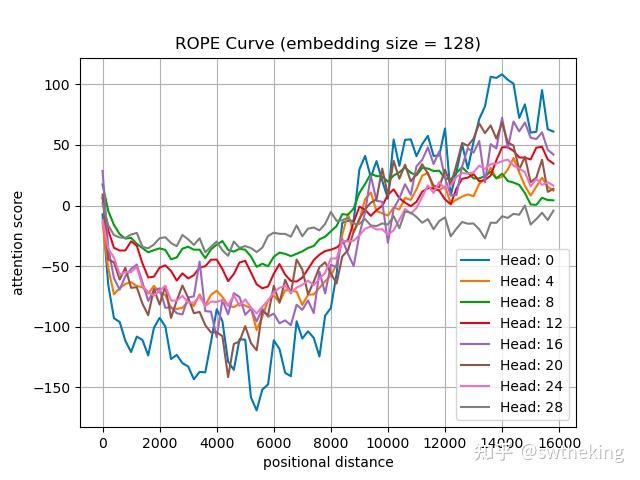
可以发现在8k前attention score 虽然不难保证严格一致下降，但依然可以保持在远端为0附近。但是出了8k以后，就开始远程上升了。当我们试着用llama-3.1-64k rope_base = 8000000, 在不训的情况下，整体曲线变成：

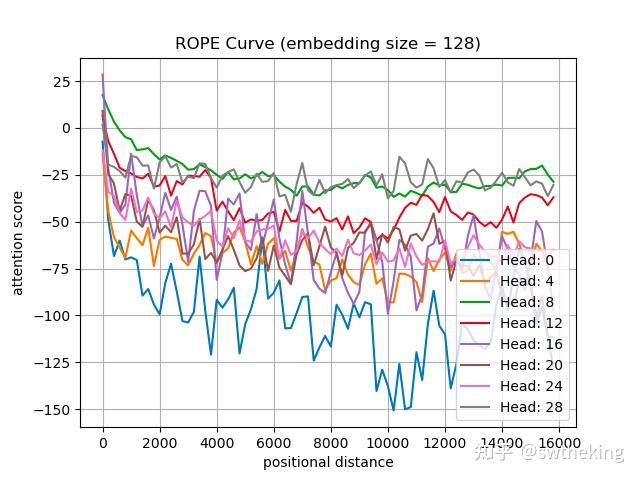
那么明显16k以内可以保证远程衰减了～。

Attention score保持远程衰减是重要的，原因是，人类语言在叙述的时候更focus在最近的n个tokens上。如果不能保持远程衰减，那么会导致你的注意力过度关注非常远的token，而忽略你刚输入的token，那么会破坏语意连续性。 比如写代码的时候，import numpy ....., if ...., el <pre>, 你需要继续预测<pre>，正常的modle会focus在el上，然后预测后面是se，组成else。如果不远程衰减，会focus在 numpy上，那么预测啥就不知道了。

如果只做到远程衰减，最差可以得到一个接近Slide window的做法： 也就是我只关注最近n个tokens，其余变为0。这种做法有个问题，那就是不能召回远端相关的tokens（也就是检索任务会不好）。那么除了远程衰减以外，position embedding需要保证attention score远程震荡为0，而不一直为0。这样就可以保证能召回非常相关的tokens，这也是RoPE的优点之一。

from：

• Site Unreachable

• Site Unreachable

ROPE后的embedding，是低频部分保持远程衰减，还是高频部分保持远程衰减？

回答：

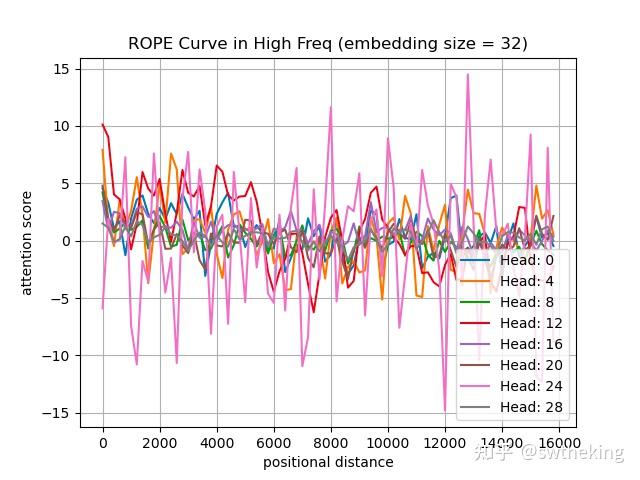
低频

在Llama-2-4k中第一层中，我们随机取了两个token，观测positional distance和 attention score的关系

在低频32维度，attention score变化如下：

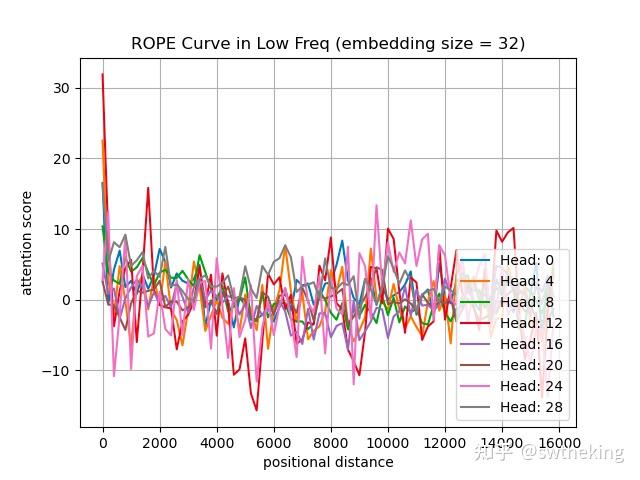
在高频32维度，attention score变化如下：

Site Unreachable

示例对比

假设查询q在位置m=2，键k在位置n=5：

• 绝对位置编码：计算注意力时需显式比较pos_2和pos_5的嵌入向量。

• ROPE：直接对q旋转2θ、k旋转5θ，点积结果自然包含相对位置差3θ，无需显式存储位置嵌入。

总结

• 一种用于Transformer模型中的相对位置编码方法，旨在通过旋转操作将位置信息融入自注意力机制，从而有效捕捉序列中元素之间的相对位置关系。

• 通过绝对位置编码的方式实现相对位置编码。将一个向量旋转某个角度，为其赋予位置信息，同时将显式的相对位置依赖性纳入自注意公式中。

• 具有较好的外推性：可以通过旋转矩阵来生成超过预训练长度的位置编码

• 具有远程衰减性质：随着相对距离的变大，内积结果有衰减趋势

• 长序列友好：旋转角度的衰减设计（如θ_i随维度指数下降）使模型能处理长程依赖

• 可以与线性注意力机制兼容：旋转操作保持向量的模长不变（因为旋转矩阵是一个正交矩阵），适合与线性注意力结合以提升效率。

• 无需额外参数：旋转矩阵由预定义规则生成，不增加可训练参数量。

参考资料

让研究人员绞尽脑汁的Transformer位置编码（介绍各种位置编码方法）

Transformer升级之路：2、博采众长的旋转式位置编码

图解 RoPE 旋转位置编码及其特性 （简单易懂，远程衰减性质）

LLM：旋转位置编码（RoPE）的通俗理解

十分钟读懂旋转编码（RoPE） （全面，介绍、代码、外推性）

再论大模型位置编码及其外推性（万字长文）(赞！)

1. 虽然RoPE理论上可以编码任意长度的绝对位置信息，但是实验发现RoPE仍然存在外推问题，即测试长度超过训练长度之后，模型的效果会有显著的崩坏，具体表现为**困惑度（Perplexity，PPL）**等指标显著上升。

2. RoPE做了线性内插（缩放位置索引，将位置m修改为m/k）修改后，通常都需要微调训练。

3. 虽然外推方案也可以微调，但是内插方案微调所需要的步数要少得多。

4. NTK-Aware Scaled RoPE非线性内插，是对base进行修改（base变成 10000⋅α ）。

5. NTK-Aware Scaled RoPE在不微调的情况下，就能取得不错的外推效果。（训练2048长度的文本，就能在较低PPL情况下，外推8k左右的长文本）

6. RoPE的构造可以视为一种 β 进制编码，在这个视角之下，NTK-aware Scaled RoPE可以理解为对进制编码的不同扩增方式（扩大k倍表示范围L->k*L，那么原本RoPE的β进制至少要扩大成 β(kd/2) 进制）。